Hakuin Zenji occupying the ground he sits on. Where is he?

Heisenberg’s Uncertainty Principle!

Most of us are uncertain about this or that. In quantum mechanics uncertainty isn’t a matter of confidence or knowledge, it is in the nature of the beast.

I am often amazed how this uncertainty principle is seen by scientists as such a strong principle that observations and outcomes must obey it. No questions asked, no reservations.

Here’s what it says:

There are measurements, things you can know about a particle, say a photon or electron. Some of these come in pairs such that both cannot be known to the same degree of certainty at the same time. Period. Our ability to measure the universe with our senses (and our devices which are extensions of our senses), what we can know by observation, is fundamentally limited.

Often it is said that this is due to the clumsiness and coarseness of our measuring devices. Send in a photon to “see” where the electron is by pinging it, and you now have an interaction that changes things. The size and energy of what you use to “touch” the world of particles is so large proportional to the particles, you can’t help but disturb it, to change it as you measure it.

Fair enough.

But it in fact goes more deep than that.

Lets look at momentum and position.

Momentum is how much oomph something has when it is moving, how much bang it would have if it hit something. If the object has mass, momentum is simply mass times velocity. The more massive the object and faster it is going in a specific direction (velocity is speed and direction, a very important point), the more momentum it has. Since photons have no mass, the momentum is a function of its energy, or wavelength, but that matters little to us here. The idea is the same, directed energy, how much oomph it has in a specific direction.

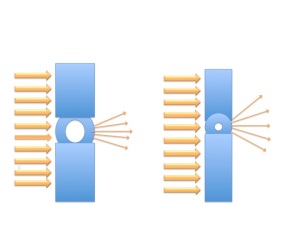
Lets look at an experiment, shining light at holes in the screen. The light is represented by the golden arrows going left to right.

If we shine a wide beam of light with many photons against a screen that has a hole in it, most of the light is spread out pretty evenly along the screen and will hit the screen pretty evenly all over (well, an area of the screen as large as the beam is). We don’t know where in that beam a given photon is exactly. It is in the room between the light source and the screen it was aimed at, but a given photon can be positioned anywhere in the beam of light (the straight arrows to the left of the screens in the illustration).

But assuming we know the wavelength of the light, and the direction the beam was pointed, we know the momentum of any photon in that beam with a great deal of accuracy. The beam was directed toward the screen, and so if undisturbed should be going pretty straight on (except for the stray cosmic ray or atom in the air hitting the beam, for example, pretty small effects here and they can be minimized), and at the speed of light in air, and so we pretty much know speed and direction pf the beam and so all the photons in it. So while the momentum of individual photons will vary a bit, it won’t be by much.

We can say then that before the light gets to the screen we have little (but some) information about position of the photons in the light, but a lot of information about momentum of the photons.

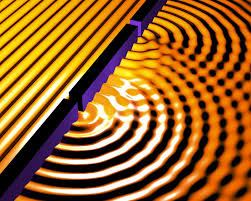
Next, some of the light goes through the hole on the screen at the left in our illustration. There is a phenomenon called diffraction. When the light leaves the hole, it bends out at the edges. The larger the hole, the less relative bending, the smaller the hole the more bending. Picture a broad water wave going through a small opening in a jetty. On the other side of the hole in the jetty the wave will expand. If it is a big hole, most of the water wave just goes right through undisturbed, only the part of the wave right at the edge of the opening in the jetty is going to spread out again after passing through. So big opening less relative rate of spreading.

A broad wave on the left goes through the holes and then spreads out. This is another way to see diffraction. In this case there are two holes and so the diffracting waves interfere. We will limit ourselves to one hole this post!

 

Our light now goes through the hole in the screen on the left below.

Only about two arrows from the light on the left enter the hole. We know where the hole is, so now we have a lot more information about position of photons just after they enter and and right after they exit the hole than we had before the light entered the hole. We know pretty well where that light (and any given individual photon in the light beam) in the hole is when it is in the hole or just after it exits the hole so we know with a high probability where a photon that is going through the hole or just exited will be found, much more so than before the light entered the hole.

But due to diffraction induced by the hole when the light exits the hole (to the right in the illustration) the beam spreads out. But at that point, at the exit of the hole, that tails of the arrows are close together, and the area the photons can likely be found is about the size of the hole, so we still have information about position that is much more precise than before. An important point is that it right after the hole at the base of the arrow that matters. It is the direction of the arrow, not what is happening at the tip that counts here. What we see though is that only the central arrows of light are still going in the same direction that they were before entering the hole, as they were not affected by the edges of the hole (really mostly the most central arrow) and are not diffracted. So while we know we will find a given photon in the area about the size of the hole, if it was at the edge of the beam its direction (hence momentum) will have changed considerably. So some photons have the same momentum, but many have changed. We are less certain about momentum because remember, momentum isn’t just speed (the speed of light didn’t change) but also direction (and that for many photons that has changed due to diffraction at the edge of the hole).

We went from knowing little about the position, and a lot about the momentum, to knowing a lot about the position and much less about the momentum of a given photon. The possibilities for position have decreased, the possibilities for the momentum have increased.

On the illustration above, we made the hole in the screen on the right smaller. Now only one arrow from the light coming in from the left  gets through. You guessed it, we then have more information about position on the other side of the hole. It is confined to a smaller area due to the smaller hole. But since the hole is smaller, on leaving the hole there is more diffraction,a large proportion of photons are diffracted (there is less “middle” of the beam for them to avoid being diffracted; by the way it is of course much more compacted than that; but it is a good enough model to have in our heads for us to see what is going on), and the arrows are more widely directed, pointing at more of an angle from the smaller hole than the larger hole (now rather than three almost undisturbed as in the screen at the left, only one goes through unscathed) as there is more hole edge effect (diffraction) for the size of the hole. That is how diffraction works, it increases the smaller the hole.

More diffraction, more range of momenta.

In fact a door in a room diffracts light coming through it and bends it, so light goes around corners just like sound goes around corners. In fact, YOU diffract! But the effect is so small we can not perceive it.

Now with the smaller hole we have even more information about position but less about the momentum. We know with greater certainty where a given photon is likely to be, but even less about what its momentum is. We still know something about the momentum, we are just less certain for a given photon use precisely what it is.

We see this in the graphs. The up axis of the graph (the thin axis arrow pointing up) is the spread of possible momentums, higher up is more momentum. The axis going left to right (the thin axis arrow pointing to the right) is the spread of possible positions. It is simply where the beam is, so where a photon may be found. So the larger our rectangle is up and down, the larger our spread of possible momenta (our uncertainty for a given photon is larger) and the wider the rectangle, the larger our spread of possible positions, (our uncertainty about position is larger).

Graphs of possible states of momentum (up and down), and position (left to right), for the light before it enters the hole (left graph), the large hole (center graph) and the small hole (right graph) .

 

In the graph on the left, we see a wide spread of potential positions, but a narrow band of momenta. This is the beam before it goes through the hole. So we end up with a narrow rectangle in blue; narrow up and down as momentum is pretty well known (reflecting little uncertainty about the momentum of any given photon in the beam) but very long left and right (reflecting great uncertainty as to just where a photon may be as the beam is wider than the hole before going through the hole).

In the middle graph, we see the situation as the light exits the larger hole. We know less about momentum, so the square is larger up and down, reflecting more uncertainty about momentum due to diffraction and the new direction the light can take. There are now more momenta a photon can have, more directions. New directions means new momenta. On the other hand, we know more about the possible position of the photons because where they are as they exit the hole is limited by the size of the hole, and this is a smaller hole, limiting where they are likely to be, so the rectangle is narrower left and right. We are less uncertain as to where the photon is; it just left the hole so that limits where we are likely to find it, outside of effects like quantum tunneling, a subject for later!

The graph on the right is what happens after light passes through the smaller hole. We are more certain about the possible positions of the photons as this is limited by the smaller size of the hole, so the rectangle is narrower left and right, but we are more uncertain about momentum (more diffraction changing the direction) so the rectangle is wider up and down.

The area of the square and how this area is distributed is the critical thing to look at. Areas in calculus are the “integral,” in this case “integrating” (summing up) our knowledge of possible values for momentum and position in our experimental set up, as it were. Making them squares of one density is too simple of course. The potential state of the photon may not be equally likely to be anywhere in the square. Some states are more likely than others. The likely position, for example, may be more concentrated in the center just opposite the hole. But I wanted to introduce a way to see very important and mathematically sophisticated quantum ideas. The area of the square is the “probability density” of where you will likely find the photon and what its momentum may be in this “space of states,” (that is official quantum jargon) that is, the space, or dimensions, of momentum and position in our experimental set up.

A quantum scientist can never speak about how it “REALLY is” just what is the range of possibilities given your experiment. This relates to integral calculus and Fourier transforms. It relates to the very heart of quantum mechanics. (Congratulations). Much of a course in quantum mechanics is solving such problems of the space of states in a given situation and the areas that reflect probabilities.

These quantum effects, this uncertainty of the “material” world, just like diffraction at a doorway, are real for you and me and cars and galaxies. We can’t see them, as they are very small at the scale of our sensory apparatus (eyes). We think we can look at the speedometer of our car and the direction we are driving and where we are on the road and know both momentum and position, but even there, as soon as we note all that, it has changed. But even if we have a set up that can look at all of this data simultaneously (a whole discussion right there) it would be changing not only because it takes time to observe and note all of these things, a computer can do that very quickly, but because there is no difference between us and the quantum world other than what our limitations as embodied beings relying on sense impressions at our scale imposes.

That is, you don’t know both your position and momentum with 100% accuracy. Just well enough to get through the door (well, and then some).

An interesting implication of this is quite consistent with the Buddhist teachings about change and impermanence. There is never no movement. Not at absolute zero, not ever. If there were no movement it would violate the uncertainty principle. We would know position exactly (wherever we froze the particle) and momentum exactly (no momentum if it isn’t moving!). Really, that’s what I meant at the beginning. This principle is so basic, so essential in the math as well as our observations, that scientists will not allow it to be breached. Like conservation of energy, it is foundational in science.

So what does it mean to me? Is it cool that some aspect of Buddhist philosophy has scientific validation? Sure, I like that, but that isn’t all that important really I think. It also is a taste of the unreasonable ability of math (that was very, very sophisticated math back there) to reflect reality.

And more importantly, as before, it reminds us that what we see, what we can determine about the nature of reality using our senses, is dependent on our limitations, our projections, our assumptions. The concepts, words and intuitions we have developed in the 4 dimensional world of space and time are mere approximations. Don’t get too attached to them. That is what this aspect of the quantum world says to me.

Fluid.

There is no fixed place.

Ever.

Heisenberg’s Uncertainty Principle!